The Use of Dijkstra's Algorithm in Determining the Shortest Path of Expedition in Bandarlampung

Article Sidebar

FULL TEXT PDF
Published: Nov 13, 2024
DOI: https://doi.org/10.26554/integrajimcs.20241323
Keywords:
Dijkstra’s Algorithm, Shortest Path, Expeditions, J&T Express

Main Article Content

Adelia Assiva
Department of Mathematics, Faculty of Mathematics and Natural Science, Universitas Lampung, Lampung, 35145, Indonesia
Resta Meyliana Puspita
Department of Mathematics, Faculty of Mathematics and Natural Science, Universitas Lampung, Lampung, 35145, Indonesia
Riska Romauli Sihombing
Department of Mathematics, Faculty of Mathematics and Natural Science, Universitas Lampung, Lampung, 35145, Indonesia
Siti Laelatul Chasanah
Department of Mathematics, Faculty of Mathematics and Natural Science, Universitas Lampung, Lampung, 35145, Indonesia
Mira Mustika
Department of Mathematics, Faculty of Sciences, Institut Teknologi Sumatera, Lampung, 35365, Indonesia

Abstract

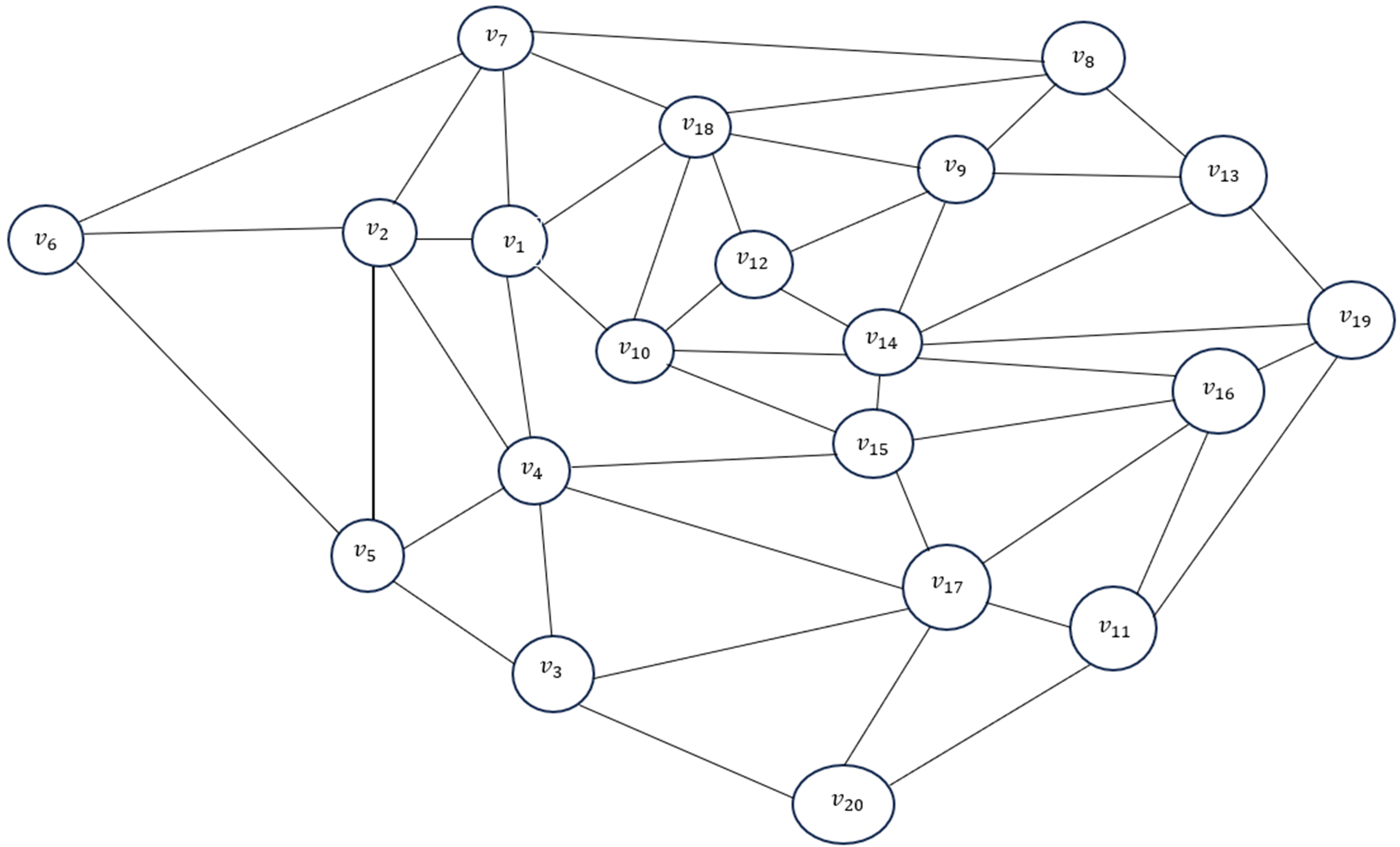
Delivery of goods is a problem faced by freight forwarders/expedition companies. Determining an efficient route will determine the speed and cost of delivery. This is faced by most expedition companies, including one of the expedition companies in the city of Bandarlampung, namely the J&T Express expedition. There are 20 J&T Express branches in Bandarlampung city. If someone wants to send an item but one of the branches is closed or not available then he will try to determine the next closest branch. In this study, the shortest path from J&T on Pagar Alam to 19 other branches in Bandarlampung will be determined using Dijkstra’s Algorithm.

Article Details

Issue
Vol. 1 No. 3 (2024): November
Section
Articles

References

[1] R.D. Gunawan and R. Napianto. Implementation of Dijkstra’s algorithm in determining the shortest path (case study: Specialist doctor search in Bandarlampung). International Journal of Information Systems and Computer Science, 3(3):98–106, 2019.

[2] Alexander Schrijver. On the history of the shortest path problem. Documenta Mathematica, 17:155–167, 2012.

[3] S.R. Aulia, Wamiliana, Asmiati, and Notiragayu. Perbandingan algoritma Dijkstra dan algoritme A dalam penentuan lintasan terpendek dari Dinas Pendidikan Provinsi Lampung ke beberapa Sekolah Menengah Atas (SMA) Negeri di Provinsi Lampung*. Jurnal Pepadun, 4:83–190, 2023.

[4] P.H. Nurhandayani, Wamiliana, Misgiyati, Notiragayu, and Muslim Ansori. The comparison of Dijkstra’s algorithm and Floyd–Warshall’s algorithm to determine the shortest path of traditional markets in Bandarlampung City. Explore, 15(1):131–139, 2024.

[5] A.D. Putriani, Wamiliana, and S.L. Chasanah. Comparison of the Dijkstra’s algorithm and the Floyd–Warshall’s algorithm to determine the shortest path between hospitals in several cities in Lampung Province. Journal of Mathematical Sciences and Optimization, 1(2):44–52, 2024.

[6] A.D. Rudiyanto, M.I. Wahyuddin, and Andrianingsih. Perbandingan algoritma Floyd–Warshall dan Dijkstra untuk menentukan lintasan rumah sakit terdekat dalam lintasan evakuasi kecelakaan lalu lintas berbasis web. Journal of Information Technology and Computer Science, 3:336–345, 2020.

[7] C.S. Rahayu, W. Gata, S. Rahayu, A. Salim, and A. Budiarto. Penerapan algoritma Dijkstra dalam penentuan lintasan terpendek menuju UPT Puskesmas Cilodong, Kota Depok. Jurnal Teknik Informatika, 14(1):81–92, 2022.

[8] P. Sembiring, A.S. Harahap, and K.S. Zalukhu. Implementation of Dijkstra’s algorithm to find an effective route to avoid traffic jam on a busy hour. In IOP Conference Series: Materials Science and Engineering, volume 1116, page 022042, 2018.

[9] A. Cantona, F. Fauziah, and W. Winarsih. Implementasi algoritma Dijkstra pada pencarian lintasan terpendek ke museum di Jakarta. Jurnal Teknologi dan Manajemen Informatika, 6(1):27–34, 2020.

[10] N.Z. Kai, Yao-Ting, and M. Yue-Peng. Shortest-path analysis based on Dijkstra’s algorithm in emergency response system. Telkomnika Indonesian Journal of Electrical Engineering, 12(5):3476–3482, 2014.

[11] L.Y. Sipayung, C.R. Sinaga, and A.C. Sagala. Application of Dijkstra’s algorithm to determine the shortest route from city center to Medan City tourist attractions. Journal of Computer Networks, Architecture and High Performance Computing, 5(2):648–655, 2023.

[12] Y. Darnita, R. Toyib, and Rinaldi. Implementasi algoritma Floyd–Warshall untuk menentukan letak dan lokasi perusahaan travel/rental mobil di Kota Bengkulu. Jurnal Pseudocode, 4:144–155, 2017.

[13] G. Rachmawati and L. Gustin. Analysis of Dijkstra’s algorithm and A algorithms in shortest path problem*. Journal of Physics: Conference Series, 1566(1):012061, 2020.

[14] V.N.C. Sebayang and I. Rosyida. Implementations of Dijkstra’s algorithm for searching the shortest route of ojek online and a fuzzy inference system for setting the fare based on distance and difficulty of terrain (case study: in Semarang City, Indonesia). In Proceedings of the International Conference on Mathematics, Geometry, Statistics, and Computation (ICMaGeStiC 2021), volume 96, pages 76–84, 2022.

[15] M.C. Bunaen, H. Pratiwi, and Y.F. Riti. Penerapan algoritma Dijkstra untuk menentukan rute terpendek dari pusat Kota Surabaya ke tempat bersejarah. Jurnal Teknologi dan Sistem Informasi Bisnis, 4(1):213–223, 2022.

[16] T. Triase and R. Aprilia. Implementasi penyaluran paket online shop menggunakan algoritma FIFO dan Dijkstra. Query: Journal of Information Systems, 4(1):60–67, 2020.

[17] R. Yuliantari and L. Musabbikhah. Review artikel: Analisis penggunaan algoritma Dijkstra untuk mencari rute terpendek di rumah sakit. Edu Elektrika Journal, 11(1):1–5, 2022.

[18] P. Sharma and N. Khurana. Study of optimal path-finding techniques. International Journal of Advances in Technology, 4(2):124–130, 2013.

[19] Wamiliana. Minimum Spanning Tree dan Desain Jaringan. Pusaka Media, Bandarlampung, 2022.

[20] A. Majeed and I. Rauf. Graph theory: A comprehensive survey about graph theory applications in computer science and social networks. Inventions, 5(1):10, 2020.