Comparative Analysis of CIH and Christofides Algorithms for Optimal Tourist Route Planning in West Java

Article Sidebar

FULL TEXT PDF
Published: Jul 31, 2025
DOI: https://doi.org/10.26554/integrajimcs.20252231
Keywords:
TSP, Cheapest Insertion Heuristic, Christofides, Recreational Spot, West Java

Main Article Content

Nur Wafiqoh Hadi
Department of Mathematics, Faculty of Mathematics and Natural Sciences, University Lampung, Lampung, 35145, Indonesia
Rehsya Nurfabella
Department of Mathematics, Faculty of Mathematics and Natural Sciences, University Lampung, Lampung, 35145, Indonesia
Wamiliana
Department of Mathematics, Faculty of Mathematics and Natural Sciences, University Lampung, Lampung, 35145, Indonesia
Mira Mustika
Department of Mathematics, Faculty of Sciences, Institut Teknologi Sumatera, Lampung, 35365, Indonesia

Abstract

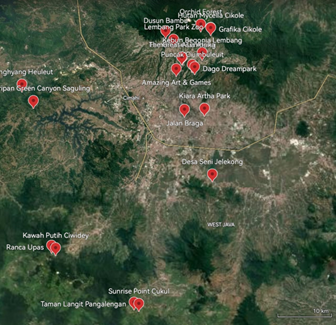
Efficient route planning plays a crucial role in supporting tourism development, particularly in regions with numerous scattered attractions such as West Java, Indonesia. This study addresses the Traveling Salesman Problem (TSP) by comparing two algorithmic approaches: the Cheapest Insertion Heuristic (CIH) and the Christofides algorithm, to determine the shortest tour among 20 selected tourist sites. Using travel time data obtained from Google Maps, both algorithms were implemented manually and using Python language programming. The manual application of the CIH algorithm resulted in a total travel time of 813 minutes, which was later optimized to 764 minutes after adjustments to eliminate intersecting paths. Meanwhile, the CIH algorithm implemented in Python provided a final route of 717 minutes. In contrast, the Christofides algorithm yielded consistent results for both manual and Python-based calculations, producing a tour with a total travel time of 746 minutes. The findings suggest that the CIH algorithm using Python language offers the most efficient route in this case study. This research contributes to the development of intelligent tour planning systems and can be a valuable reference for optimizing regional tourism logistics.

Article Details

Issue
Vol. 2 No. 2 (2025): July
Section
Articles

References

[1] Hasana Fadilla. Pengembangan Sektor Pariwisata untuk Meningkatkan Pendapatan Daerah di Indonesia. Benefit: Journal of Bussiness, Economics, and Finance, 2(1):36–43, 2024.

[2] Miko Purnomo, Justin Eduardo Simarmata, and Debora Chrisinta. Optimasi Jarak Terpendek untuk Mencapai Wisata Super Prioritas Indonesia dengan Menggunakan Pendekatan Traveling Salesman Problem. MathVision: Jurnal Matematika, 7(1):53–61, 2025.

[3] Christoph Hansknecht, Imke Joormann, and Sebastian Stiller. Dynamic Shortest Paths Methods for the Time-Dependent TSP. Algorithms, 14(1):21, 2021.

[4] Nasywa Shafa Azzahra, Najwa Nayra Aulia, Arista Binarsih, and P. Paduloh. Analisis Optimasi Jalur Distribusi Menggunakan Pendekatan TSP (Traveling Salesman Problem) untuk Meningkatkan Efisiensi Biaya Distribusi Pada Toko Uthe Grosir. HUMANITIS: Jurnal Homaniora, Sosial Dan Bisnis, 2(6):542–553, 2024.

[5] Sriyani Violina. Analysis of Brute Force and Branch & Bound Algorithms to Solve the Traveling Salesperson Problem (TSP). Turkish Journal of Computer and Mathematics Education, 12(8):1226–1229, 2021.

[6] Md Ziaur Rahman, Sakibur Rahamn Sheikh, Ariful Islam, and Md Azizur Rahman. Improvement of the Nearest Neighbor Heuristic Search Algorithm for Traveling Salesman Problem. Journal of Engineering Advancements, 5(01):19–26, 2024.

[7] Noraini Mohd Razali, John Geraghty, et al. Genetic Algorithm Performance with Different Selection Strategies in Solving TSP. In Proceedings of the World Congress on Engineering, volume 2, pages 1–6. International Association of Engineers, Hong Kong, China, 2011.

[8] Xuesong Yan, Can Zhang, Wenjing Luo, Wei Li, Wei Chen, and Hanmin Liu. Solve Traveling Salesman Problem Using Particle Swarm Optimization Algorithm. International Journal of Computer Science, 9(6):264–271, 2012.

[9] S. Dhanasekar, Saroj Kumar Dash, and Neena Uthaman. A Branch and Bound Algorithm to Solve Travelling Salesman Problem (TSP) with Uncertain Parameters. Mathematics and Statistics, 10(2):358–365, 2022.

[10] Murat Sahin. Solving TSP by Using Combinatorial Bees Algorithm with Nearest Neighbor Method. Neural Computing and Applications, 35(2):1863–1879, 2023.

[11] Dwi Rizka Amelia Putri, Niken Sabella Oktavia, Siti Laelatul Chasanah, Riza Sawitri, and Felicia Andrade Paskalia. Implementation of Christofides Algorithm to Determine the Shortest Tour of Some Hospitals in Palembang City. Integra: Journal of Integrated Mathematics and Computer Science, 2(1):15–19, 2025.

[12] Micelle Yap Aswin, Wamiliana Wamiliana, Fitriani Fitriani, Muslim Ansori, and Notiragayu Notiragayu. Perbandingan Cheapest Insertion Heuristic dan Algoritma Christofides untuk Menentukan Tour Pasar Tradisional di Kota Bandar Lampung. Jurnal Pepadun, 5(2):182–194, 2024.

[13] Etza Nofarita Nofarita. The Utilization of the Best First Search Algorithm in the Solution of the Traveling Salesman Problem Case in City X. IJISTECH (International Journal of Information System and Technology), 5(4):360–365, 2021.

[14] Xuan-Shi Yao, Yun Ou, and Kai-Qing Zhou. TSP Solving Utilizing Improved Ant Colony Algorithm. In Journal of Physics: Conference Series, volume 2129, page 012026. IOP Publishing, 2021.

[15] Annisa Salsabila, Nadhir Rotun Nikmah, Rafif Syadid Bakhtiananda, Micelle Yap Aswin, and Dina Eka Nurvazly. Products Distribution from Suppliers to Retailers in Bandarlampung City (Case Study: Retailers Location in Teluk Betung). Integra: Journal of Integrated Mathematics and Computer Science, 1(1):6–12, 2024.

[16] Abdi Restu Dinata, Wamiliana Wamiliana, Muslim Ansori, Fitriani Fitriani, and Notiragayu Notiragayu. Determining the Shortest Tour Location of Tourist Attractions in Bandar Lampung Using Cheapest Insertion Heuristic (CIH) and Modified Sollin Algorithm. Jurnal Pepadun, 6(1):92–102, 2025.

[17] K. Pavani, M. Anitha, and B. Priyanka. Delivery Route Optimization Using Dijkstra’s Algorithm for the Travelling Salesman Problem. International Journal of Advance Scientific Research, 9(6), 2025.

[18] Farid Fargiana, Respitawulan Respitawulan, Yusuf Fajar, Didi Suhaedi, and Erwin Harahap. Implementation of Cheapest Insertion Heuristic Algorithm in Determining Shortest Delivery Route. International Journal of Global Operations Research, 3(2):37–45, 2022.

[19] Rizki Putra Sinaga and Faridawaty Marpaung. Perbandingan Algoritma Cheapest Insertion Heuristic dan Nearest Neighbor dalam Menyelesaikan Traveling Salesman Problem. Jurnal Riset Rumpun Matematika dan Ilmu Pengetahuan Alam, 2(2):238–247, 2023.

[20] Ahya Sofa Ananda, Notiragayu Notiragayu, Wamiliana Wamiliana, and Muslim Ansori. Penentuan Lintasan Terpendek Perjalanan Pengiriman Barang Menggunakan Algoritma Cheapest Insertion Heuristic (Studi Kasus PT. Indah Logistik Cargo Bandar Lampung). Jurnal EurekaMatika, 11(2):111–120, 2023.

[21] Jogamohan Medak. Review and Analysis of Minimum Spanning Tree Using Prim’s Algorithm. International Journal of Computer Science Trends and Technology, 6(2), 2018.

[22] Jiayu Chen. The Analysis and Application of Prim Algorithm, Kruskal Algorithm, Boruvka Algorithm. Applied and Computational Engineering, 19:84–89, 2023.

[23] Dian Rachmawati, Frederik Yan Putra Pakpahan, et al. Comparative Analysis of the Kruskal and Boruvka Algorithms in Solving Minimum Spanning Tree on Complete Graph. In 2020 International Conference on Data Science, Artificial Intelligence, and Business Analytics (DATABIA), pages 55–62. IEEE, 2020.