Application of GSTARMA Spatial-Temporal Model for Inflation Analysis in South Sulawesi Province

Article Sidebar

FULL TEXT PDF
Published: Nov 13, 2024
DOI: https://doi.org/10.26554/integrajimcs.20241322
Keywords:
GSTARMA, Spatial-temporal Model, Inflation, South Sulawesi Province

Main Article Content

Dede Ratna Sari
Department of Mathematics, Faculty of Mathematics and Natural Sciences, Universitas Lampung, Lampung, 35145, Indonesia
Widiarti
Department of Mathematics, Faculty of Mathematics and Natural Sciences, Universitas Lampung, Lampung, 35145, Indonesia
Dina Eka Nurvazly
Department of Mathematics, Faculty of Mathematics and Natural Sciences, Universitas Lampung, Lampung, 35145, Indonesia
Mustofa Usman
Department of Mathematics, Faculty of Mathematics and Natural Sciences, Universitas Lampung, Lampung, 35145, Indonesia
Luvita Loves
Department of Mathematics, Faculty of Science and Technology, Universitas Pattimura, Ambon, 97233, Indonesia

Abstract

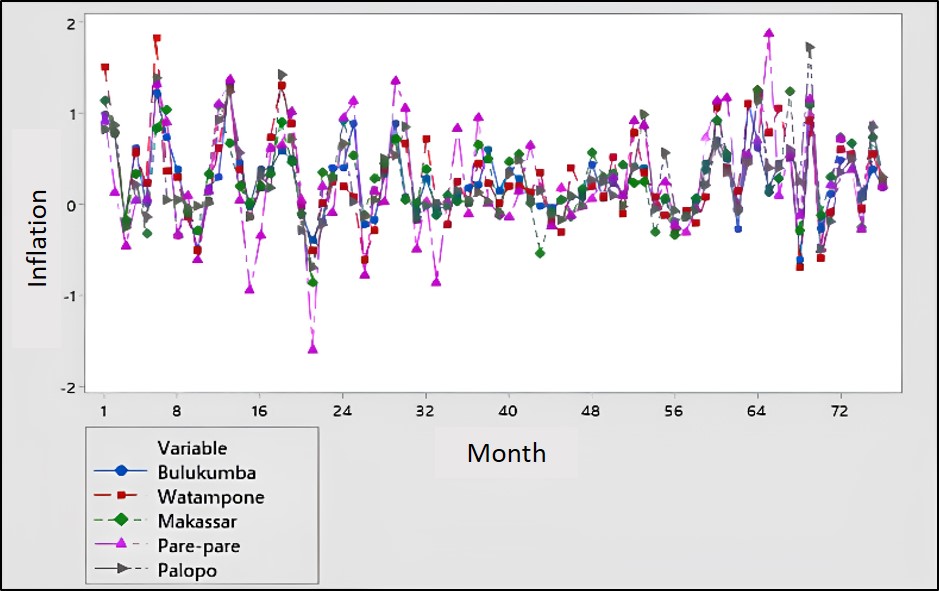
The Generalized Space-Time Autoregressive Moving Average (GSTARMA) model is a development of the time series model that can capture both spatial and temporal dynamics simultaneously. This study uses the GSTARMA model to analyze inflation data in five cities in South Sulawesi Province from January 2017 to October 2024. The GSTARMA model obtained is GSTARMA (1,0,1) with a cross-correlation normalization spatial weight matrix. The results of the analysis indicate a spatial influence between locations and temporal relationships in the inflation data.

Article Details

Issue
Vol. 1 No. 3 (2024): November
Section
Articles

References

[1] G. E. P. Box, G. M. Jenkins, G. C. Reinsel, and G. M. Ljung. Time Series Analysis: Forecasting and Control. John Wiley & Sons, Hoboken, 5th edition, 2016.

[2] W. W. S. Wei. Time Series Analysis: Univariate and Multivariate Methods. Pearson Education, USA, 2nd edition, 2006.

[3] D. Munandar, B. N. Ruchjana, A. S. Abdullah, and H. F. Pardede. Integration gstarima with deep neural network to enhance prediction accuracy on rainfall data. Systems Science & Control Engineering, 12(1), 2024.

[4] A. B. Salsabila, B. N. Ruchjana, and A. S. Abdullah. Development of the gstarima(1,1,1) model order for climate data forecasting. International Journal of Data and Network Science, 8:773–788, 2024.

[5] A. Safira, R. A. Dhiya’ulhaq, I. Fahmiyah, and M. Ghani. Spatial impact on inflation of Java Island prediction using autoregressive integrated moving average (ARIMA) and generalized space-time ARIMA (GSTARIMA). MethodsX, 13:102867, 2024.

[6] P. Monika, B. N. Ruchjana, A. S. Abdullah, and R. Budiarto. Integration of GSTARIMA model with heteroskedastic error and kriging for climate forecasting: A systematic review. Applied Mathematics & Information Sciences: An International Journal, 18(3):551–567, 2024.

[7] N. Aulia and D. R. S. Saputro. Generalized space-time autoregressive integrated moving average with exogenous (GSTARIMA-X) models. In Journal of Physics: Conference Series, volume 1808, page 012052, 2021.

[8] M. S. Akbar, Setiawan, Suhartono, B. N. Ruchjana, D. D. Prastyo, A. Muhaimin, and E. Setyowati. A generalized space-time autoregressive moving average (GSTARMA) model for forecasting air pollutant in Surabaya. In Journal of Physics: Conference Series, volume 1490, page 012022, 2020.

[9] S. Ajobo, O. Alaba, and A. Zaenal. Generalised space-time seasonal autoregressive integrated moving average seemingly unrelated regression modelling of seasonal and nonstationary data. Scientific African, 24:e02189, 2024.

[10] P. Monika, B. N. Ruchjana, and A. S. Abdullah. GSTARIX-ARCH model with data mining approach for forecasting climate in West Java. Computation, 10(12):204, 2022.

[11] M. R. Kurniawan, U. Mukhaiyar, and S. W. Indratno. Modelling of data following a GSTARMA-X model using Kalman filter. In AIP Conference Proceedings, volume 2774, 2024.

[12] U. Mukhaiyar, A. W. Mahdiyasah, and T. Prastoro. The generalized space-time autoregressive modelling with three dimensional of spatial weight matrix in predicting the Indonesia peatland’s water level. Environmental Science Europe, 36:180, 2024.

[13] U. S. Pasaribu, U. Mukhaiyar, M. N. Heriawan, and Y. Yundari. Generalized space-time autoregressive modeling of the vertical distribution of copper and gold grades with a porphyry-deposit case study. International Journal on Advanced Science Engineering Information Technology, 12(5):2030–2038, 2022.

[14] U. Mukhaiyar, B. I. Bilad, and S. Pasaribu. The generalized space-time autoregressive modeling with minimum spanning tree approach of weight matrix for COVID-19 case in Java Island. In Journal of Physics: Conference Series, volume 2084, page 012003, 2021.

[15] U. Mukhaiyar, F. T. Nabilah, U. S. Pasaribu, and N. M. Huda. The space-time autoregressive modelling with time correlated errors for the number of vehicles in Purbaleunyi toll gates. In Journal of Physics: Conference Series, volume 2243, page 012068, 2022.

[16] N. M. Huda and N. Imro’ah. Determination of the best weight matrix for the generalized space-time model in the COVID-19 case on Java Island. Spatial Statistics, 54:100734, 2023.

[17] F. Hestuningtias and M. H. S. Kurniawan. The implementation of the generalized space-time autoregressive model for inflation prediction. International Journal of Applied Statistics and Data Science, 3(2):176–188, 2023.

[18] N. M. Huda, U. Mukhaiyar, and U. S. Pasaribu. The approximation of generalized space-time autoregressive model for discrete cases through INAR model. In Journal of Physics: Conference Series, volume 1722, page 012100, 2021.

[19] J. Lee and D. W. S. Wong. Statistical Analysis Arcview GIS. John Wiley and Sons, New York, 2001.

[20] O. Ozcicek and W. McMilin. Lag length selection in vector autoregressive models symmetric and asymmetric lags. Applied Economics, 31:517–524, 1999.