On the Construction of Rough Quotient Modules in Finite Approximation Spaces
Main Article Content
Abstract
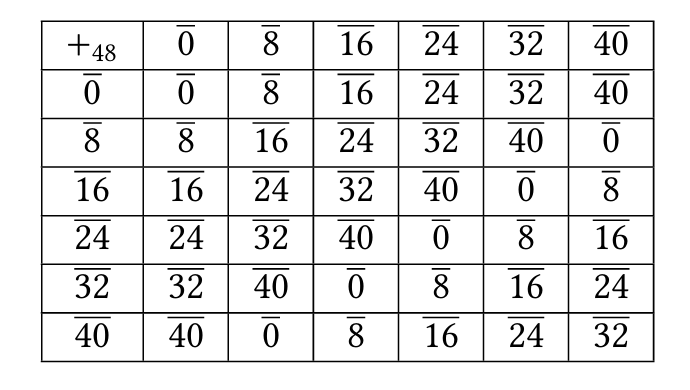
Let S be a set and φ an equivalence relation on S. The pair (S, φ) forms an approximation space, where the relation φ partitions S into mutually disjoint equivalence classes. For any subset B' ⊆ S, the lower approximation Apr(B') is defined as the union of all equivalence classes entirely contained in B', while the upper approximation Apr(B') is the union of all equivalence classes that have a non-empty intersection with B'. The subset B' is called a rough set in (S, φ) if Apr(B') ≠ Apr(B'). If, in addition, B' satisfies certain algebraic conditions, it is termed a rough module. This paper investigates the construction of rough quotient rings and rough quotient modules within such approximation spaces. The approach is developed using finite sets to facilitate the algebraic formulation and analysis of these rough structures.
Article Details
References
[1] Nurettin Bagırmaz and Abdullah F. Ozcan. Rough semigroups on approximation spaces. International Journal of Algebra, 9(7):339–350, 2015.
[2] C. A. Neelima and Paul Isaac. Rough antihomomorphism on a rough group. Global Journal of Mathematical Sciences: Theory and Practical, 6(2):79–85, 2014.
[3] Changzhong Wang and Degang Chen. A short note on some properties of rough groups. Computers & Mathematics with Applications, 59(1):431–436, 2010.
[4] A. K. Sinha and A. Prakash. Rough projective module. In Proc. of the Second Intl Conference on Advances in Applied Science and Environmental Engineering – ASEE, pages 35–38, 2014.
[5] Arvind Kumar Sinha and Anand Prakash. Injective module based on rough set theory. Cogent Mathematics, 2(1):1069481, 2015.
[6] D. Miao, S. Han, D. Li, and L. Sun. Rough group, rough subgroup and their properties. In Lecture Notes in Artificial Intelligence, number 3641, pages 104–113, 2005.
[7] Q. Zhang, A. Fu, and S. Zhao. Rough modules and their some properties. In Proceeding of the Fifth International Conference on Machine Learning and Cybernetics, pages 2290–2293, 2006.
[8] P. Isaac and U. Paul. Rough g-modules and their properties. Research India Publications, 12(1):99–100, 2017.
[9] A. A. Nugraha, Fitriani, M. Ansori, and A. Faisol. The implementation of rough set on a group structure. Jurnal Matematika MANTIK, 8(1):45–52, 2022.
[10] D. Hafifulloh, Fitriani, and A. Faisol. The properties of rough v-coexact sequence in rough group. BAREKENG: Journal of Mathematics and Its Application, 16(3):1069–1078, 2022.
[11] F. A. Agusfrianto, Fitriani, and Y. Mahatma. Rough rings, rough subrings, and rough ideals. Journal of Fundamental Mathematics and Applications (JFMA), 5(2):1–8, 2022.
[12] F. A. Agusfrianto and L. Ambarwati. Some properties of rough ideals on rough rings. Eigen Mathematics Journal, 6(1):1–4, 2023.
[13] Gusti Ayu Dwi Yanti, Fitriani, and Ahmad Faisol. The implementation of a rough set of projective module. BAREKENG: Journal of Mathematics and Its Applications, 17(2):0735–0744, 2023.
[14] Bijan Davvaz and M. Mahdavipour. Roughness in modules. Information Sciences, 176(24):3658–3674, 2006.
[15] Zhihua Chen, Saba Ayub, Waqas Mahmood, Abid Mahboob, and Chahn Yong Jung. A study of roughness in modules of fractions. IEEE Access, 7:93088–93099, 2019.
[16] Srinivasan Vijayabalaji, Shanmugam Kalaiselvan, Natesan Thillaigovindan, and Bijan Davvaz. Modified soft-rough modules and their approximations. Journal of Multiple Valued Logic & Soft Computing, 41(6), 2023.
[17] Fakhry Asad Agusfrianto, Fitriani, and Yudi Mahatma. On rough bimodules. In AIP Conference Proceedings, volume 2970, page 030002. AIP Publishing LLC, 2024.
[18] Gusti Ayu Dwi Yanti and Fitriani. On x-sublinearly independent of rough groups. Journal of the Indonesian Mathematical Society, 30(3):438–446, 2024.
[19] Fitriani, Indah Emilia Wijayanti, and Ahmad Faisol. Rough x-sub-exact sequences of rough modules. Palestine Journal of Mathematics, 13(3), 2024.
[20] Ralf Meyer. Smooth and rough modules over self-induced algebras, 2009.
[21] Rara Gusti Rahmawati, Fitriani, and Ahmad Faisol. The properties of rough submodule over rough ring. Jurnal Matematika Integratif, 20(2):185–196, 2024.