The Cleanness Property of The Integers Modulo n (ℤn)
Main Article Content
Abstract
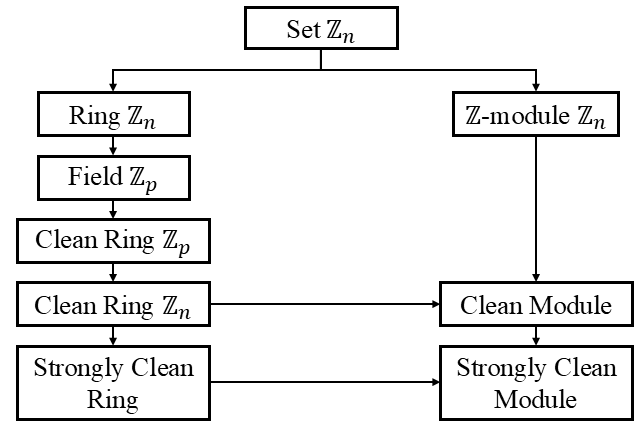
Assume that R is a ring with identity. A ring R is said to be clean when each of its elements can be written as the sum of an idempotent and a unit element within the ring. A stronger condition, known as strongly clean, requires that these elements commute under multiplication. As a special case, a module M over ring R is called a clean module when the endomorphism ring of the M is a clean module over R. Moreover, when the ring endomorphism of R-module M is a strongly clean, then the module M is referred to as a strongly clean. We know that the integers modulo n, denoted by ℤn, is a ring by the set of congruence classes modulo n, with standard addition and multiplication operations. In this study, we explore the cleanness properties of the ring ℤn and establish that it is a strongly clean ring. Furthermore, we study about the cleanness of ℤn as a module over ℤ and investigate the strongly cleanness of it module.
Article Details
References
[1] W Keith Nicholson. Lifting idempotents and exchange rings. Transactions of the American Mathematical Society, 229:269–278, 1977.
[2] Cyrenia Novella Krisnamurti. Ring bersih kanan. Ad-MathEdu: Jurnal Ilmiah Pendidikan Matematika, Ilmu Matematika dan Matematika Terapan, 5(1), 2015 (in Indonesia).
[3] WK Nicholson and Yiqiang Zhou. Clean general rings. Journal of Algebra, 291(1):297–311, 2005.
[4] Tamer Koşan, Serap Sahinkaya, and Yiqiang Zhou. On weakly clean rings. Communications in Algebra, 45(8):3494–3502, 2017.
[5] S Kar and D Das. Clean semiring. Beiträge Zur Algebra und Geometrie/Contributions to Algebra and Geometry, 64(1):197–207, 2023.
[6] Sondos Osama Hussain Jamal. Clean Like Semiring Notions and Trivial Semiring Extension. PhD thesis, Doctoral Dissertation, 2020.
[7] Dian Ariesta Yuwaningsih, Indah Emilia Wijayanti, and Budi Surodjo. On r-clean ideals. Palestine Journal of Mathematics, 12(2), 2023.
[8] Hongbo Zhang and Victor Camillo. On clean rings. Communications in Algebra, 44(6):2475–2481, 2016.
[9] Yuanlin Li and Qinghai Zhong. On clean, weakly clean and feebly clean commutative group rings. Journal of Algebra and Its Applications, 21(05):2250085, 2022.
[10] Nitin Arora and S Kundu. Commutative feebly clean rings. Journal of Algebra and its Applications, 16(07):1750128, 2017.
[11] W Keith Nicholson. Strongly clean rings and fitting’s lemma. Communications in Algebra, 27(8):3583–3592, 1999.
[12] Orhan Gurgun and Sait Halicioglu Ungor. A subclass of strongly clean rings. Communications in Mathematics, 23(1):13–31, 2015.
[13] Janez Šter. Examples of strongly clean rings. Communications in Algebra, 47(11):4684–4696, 2019.
[14] Jian Cui and Zhou Wang. A note on strongly*-clean rings. Journal of the Korean Mathematical Society, 52(4):839–851, 2015.
[15] D Das and S Kar. Strongly clean semiring. Proceedings of the National Academy of Sciences, India Section A: Physical Sciences, 94(2):249–258, 2024.
[16] Pace Nielsen and Janez Šter. Connections between unitregularity, regularity, cleanness, and strong cleanness of elements and rings. Transactions of the American Mathematical Society, 370(3):1759–1782, 2018.
[17] Gangyong Lee, Cosmin S Roman, and Xiaoxiang Zhang. Modules whose endomorphism rings are division rings. Communications in Algebra, 42(12):5205–5223, 2014.
[18] Victor P Camillo, Dinesh Khurana, TY Lam, WK Nicholson, and Y Zhou. Continuous modules are clean. Journal of Algebra, 304(1):94–111, 2006.
[19] Hongbo Zhang. On strongly clean modules. Communications in Algebra, 37(4):1420–1427, 2009.
[20] Cyrenia Novella Krisnamurti. Modul bersih kanan right clean modules. Jurnal Penelitian, 21(1):22–25, 2017 (in Indonesia).
[21] A Ismarwati, H France-Jackson, Sri Wahyuni, and IE Wijayanti. On nice modules. JP Journal of Algebra, Number Theory and Applications, 38(3):213, 2016.
[22] Yasser Ibrahim and Mohamed Yousif. Utumi modules. Communications in Algebra, 46(2):870–886, 2018.
[23] Nikken Prima Puspita, IE Wijayanti, and Budi Surodjo. Clean coalgebras and clean comodules of finitely generated projective modules. Algebra and Discrete Mathematics, 31(2):251–260, 2021.
[24] Nikken Prima Puspita, Indah Emilia Wijayanti, and Budi Surodjo. Some sufficient conditions of clean comodules. The Aligarh Bulletin of Mathematics, 41(2):1–20, 2022.
[25] Nikken Prima Puspita, Indah Emilia Wijayanti, and Budi Surodjo. Graded modules as a clean comodule. Journal of Mathematics Research, 12:66–73, 2020.
[26] Sri Wahyuni, Indah Emilia Wijayanti, Dian Ariesta Yuwaningsih, and Ari Dwi Hartanto. Teori Ring dan Modul. UGM PRESS, 2021.
[27] Robert Wisbauer. Foundations of Module and Ring Theory. Routledge, 2018.
[28] William A Adkins and Steven H Weintraub. Algebra: An Approach Via Module Theory, volume 136. Springer Science & Business Media, 2012.
[29] DS Dummit and RM Foote. Abstract algebra (2004), hoboken.
[30] Adillah Azzahra, Astuti Astuti, Adityawarman Hidayat, and Zulhendri Zulhendri. Chines remainder theorem (teorema sisa china). Integrasi Episdemik: Jurnal Multidisiplin Inovatif, 1(1):10–15, 2025.
[31] Garima Sharma and Amit B Singh. Strongly r-clean rings. International Journal of Mathematics and Computer Science, 13(2):207–214, 2018.
[32] Jianlong Chen, Xiande Yang, and Yiqiang Zhou. On strongly clean matrix and triangular matrix rings. Communications in Algebra, 34(10):3659–3674, 2006.