Implementation of Christofides Algorithm to Determine the Shortest Tour of Some Hospitals in Palembang City
Main Article Content
Abstract
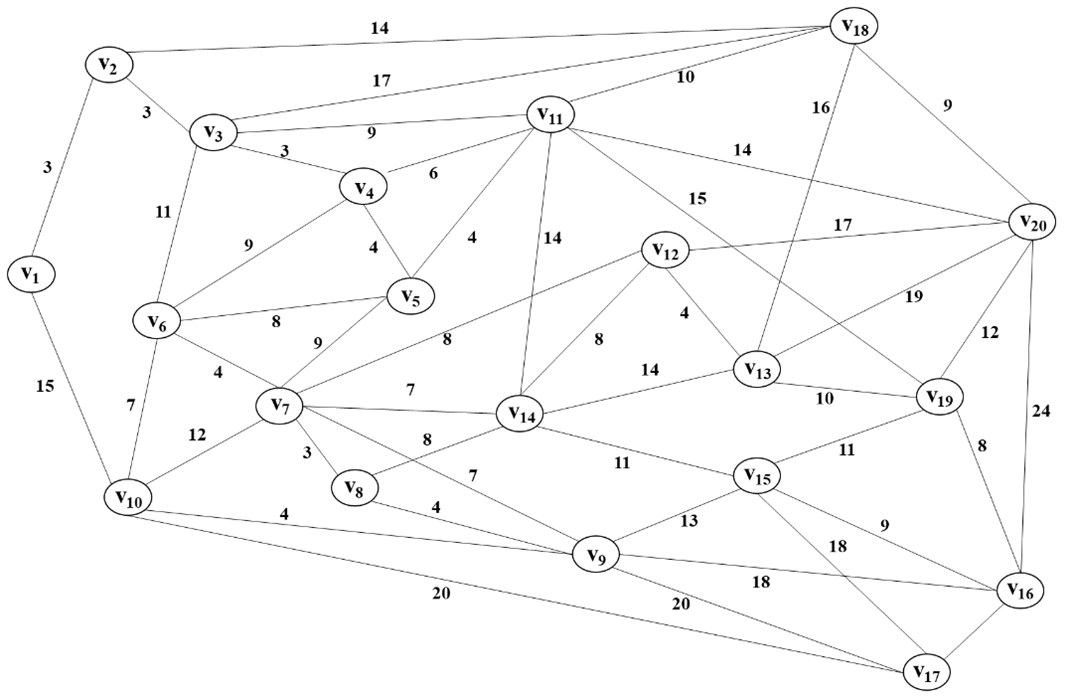
Determining the shortest route to connect hospitals is a very important aspect of improving the efficiency of medical service distribution in a big city like Palembang. The shortest tour will result in a shorter time required. This study aims to minimize the time needed for a team of technicians who want to distribute medical equipment and provide simple usage examples to some hospitals in Palembang city. There are 20 hospitals under consideration, and the data on time needed from one hospital to another were obtained from Google Maps. The distance between locations was calculated based on travel time using a four-wheeled vehicle. The Christofides Algorithm will be used in this problem to determine the shortest tour. The results show that the travel time needed is 171 minutes (only for traveling from one hospital to another and back to the origin, not including the time needed for giving the simple usage of medical equipment). This study provides practical solutions to improve time efficiency, such as delivering medical supplies or emergency response.
Article Details
References
[1] Alexander Schrijver. On the history of combinatorial optimization (till 1960). Handbooks in Operations Research and Management Science, 12:1–68, 2005.
[2] Eugene L Lawler. The traveling salesman problem: A guided tour of combinatorial optimization. Wiley Interscience Series in Discrete Mathematics, 1985.
[3] René van Bevern and Viktoriia A Slugina. A historical note on the 3/2-approximation algorithm for the metric traveling salesman problem. Historia Mathematica, 53:118–127, 2020.
[4] David B Fogel. An evolutionary approach to the traveling salesman problem. Biological Cybernetics, 60(2):139–144, 1988.
[5] Mohammad Asim, Ritika Gopalia, and Shivalika Swar. Traveling salesman problem using genetic algorithm. International Journal of Latest Trends in Engineering and Technology (IJLTET), 3(3):183–190, 2014.
[6] Gerhard Reinelt. The Traveling Salesman: Computational Solutions for TSP Applications, volume 840. Springer, 2003.
[7] Vladimir Deineko and Alexander Tiskin. One-sided Monge TSP is NP-hard. In Computational Science and Its Applications – ICCSA 2006: International Conference, Glasgow, UK, May 8-11, 2006, Proceedings, Part III 6, pages 793–801. Springer, 2006.
[8] Farid Fargiana, Respitawulan Respitawulan, Yusuf Fajar, Didi Suhaedi, and Erwin Harahap. Implementation of cheapest insertion heuristic algorithm in determining shortest delivery route. International Journal of Global Operations Research, 3(2):37–45, 2022.
[9] L Virginayoga Hignasari and Eka Diana Mahira. Optimization of goods distribution route assisted by Google Map with cheapest insertion heuristic algorithm (CIH). Sinergi, 22(2):132–138, 2018.
[10] Dian Rachmawati, Elviwani, and Asri Yulianingrum. Implementation of the cheapest insertion heuristic in determining medicine distribution routes by DP2KB Medan. In AIP Conference Proceedings, volume 2987, page 020034. AIP Publishing LLC, 2024.
[11] Annisa Salsabila, Nadhir Rotun Nikmah, Rafif Syadid Bakhtiananda, Micelle Yap Aswin, and Dina Eka Nurvazly. Products distribution from suppliers to retailers in Bandar Lampung city (case study: Retailers location in Teluk Betung). Integra: Journal of Integrated Mathematics and Computer Science, 1(1):6–12, 2024.
[12] Dian Rachmawati and Wilyanto. Implementation of modified cheapest insertion heuristic on generating Medan city tourism route. In Journal of Physics: Conference Series, volume 1566, page 012076. IOP Publishing, 2020.
[13] Abdi Restu Dinata, Wamiliana Wamiliana, Muslim Ansori, Fitriani Fitriani, and Notiragayu Notiragayu. Determining the shortest tour location of tourist attractions in Bandar Lampung using cheapest insertion heuristic (CIH) and modified Sollin algorithm. Jurnal Pepadun, 6(1):92–102, 2025.
[14] Micelle Yap Aswin, Wamiliana Wamiliana, Fitriani Fitriani, Muslim Ansori, and Notiragayu Notiragayu. Perbandingan cheapest insertion heuristic dan algoritma Christofides untuk menentukan tour pasar tradisional di Kota Bandar Lampung. Jurnal Pepadun, 5(2):182–194, 2024 (in Indonesia).
[15] Poetri Hana Nurhandayani, Wamiliana Wamiliana, Misgiyati Misgiyati, Notiragayu Notiragayu, and Muslim Ansori. The comparison of Dijkstra’s algorithm and Floyd Warshall’s algorithm to determine the shortest path of traditional markets in Bandar Lampung city. Explore: Jurnal Sistem Informasi dan Telematika (Telekomunikasi, Multimedia dan Informatika), 15(1):131–139, 2024.
[16] Stefan Hougardy and Mirko Wilde. On the nearest neighbor rule for the metric traveling salesman problem. Discrete Applied Mathematics, 195:101–103, 2015.
[17] Sitti Rosnafi’an Sumardi, Nur Nilam Sari, Justin Eduardo Simarmata, et al. Product distribution route using nearest neighbor algorithm. MALCOM: Indonesian Journal of Machine Learning and Computer Science, 4(3):894–900, 2024.
[18] Anie Lusiani, Siti Samsiyah Purwaningsih, and Euis Sartika. TSP method using nearest neighbor algorithm at PT. J&T Express in Bandung. Jurnal Lebesgue: Jurnal Ilmiah Pendidikan Matematika, Matematika dan Statistika, 4(3):1560–1568, 2023.
[19] Ulviye Hacizade and I Kaya. GA-based traveling salesman problem solution and its application to transport routes optimization. IFAC-PapersOnLine, 51(30):620–625, 2018.
[20] AB Doumi, BA Mahafzah, and H Hiary. Solving traveling salesman problem using genetic algorithm based on efficient mutation operator. Journal of Theoretical and Applied Information Technology, 99(15):3768–3781, 2021.
[21] Darius Bethel and Hakki Erhan Sevil. Revisiting traveling salesman problem (TSP): Analysis of GA and SA based solutions. International Journal of Recent Contributions from Engineering Science & IT (IJES), 9(2):44–56, 2021.
[22] Felix Tjoea and Siana Halim. Evaluasi rute pelayaran kapal dengan pendekatan modified minimum spanning tree. Jurnal Titra, 11(2):265–272, 2023 (in Indonesia).
[23] Zhou Xu and Brian Rodrigues. An extension of the Christofides heuristic for the generalized multiple depot multiple traveling salesmen problem. European Journal of Operational Research, 257(3):735–745, 2017.